Leer el siguiente texto a posterior ver el video y luego debate con tus compañeros de grupo.
De lo debatido, realiza un escrito, indicando a que conclusiones llegaron.
¿Las matemáticas se descubrieron o se inventaron?
Desde la antigüedad, la humanidad ha debatido acaloradamente sobre si las matemáticas se descubrieron o se inventaron. ¿Existirían las matemáticas si las personas no existieran?
¿Creamos conceptos matemáticos para entender el universo que nos rodea o las matemáticas son el lenguaje nativo del universo que existe aunque descubramos o no sus verdades?
Los números, los polígonos y las ecuaciones ¿son reales o meras representaciones de un ideal teórico?
La realidad "independiente" de las matemáticas tiene antiguos defensores. Los pitagóricos griegos del siglo V creían que los números eran tanto entidades vivientes, como principios universales. Llamaron al número uno, la mónada, el generador de todos los otros números y la fuente de toda creación. Para los pitagóricos, los números eran agentes activos en la naturaleza. Platón sostenía que los conceptos matemáticos eran concretos y tan reales como el universo mismo, independientes de nuestro conocimiento de ellos.
Los números, los polígonos y las ecuaciones ¿son reales o meras representaciones de un ideal teórico?
La realidad "independiente" de las matemáticas tiene antiguos defensores. Los pitagóricos griegos del siglo V creían que los números eran tanto entidades vivientes, como principios universales. Llamaron al número uno, la mónada, el generador de todos los otros números y la fuente de toda creación. Para los pitagóricos, los números eran agentes activos en la naturaleza. Platón sostenía que los conceptos matemáticos eran concretos y tan reales como el universo mismo, independientes de nuestro conocimiento de ellos.
Euclides, el padre de la geometría, creía que la naturaleza en sí misma era la manifestación física de las leyes matemáticas.
Otros argumentaron que aunque los números pueden o no existir físicamente, los enunciados matemáticos definitivamente no. Sus valores de verdad se basan en las reglas que los humanos crearon. Desde esta perspectiva, las matemáticas son, pues, un ejercicio de lógica inventado que no existe fuera del pensamiento consciente humano. Así, la matemática sería un lenguaje de relaciones abstractas basado en patrones discernidos por cerebros, construido para usar esos patrones e inventar un orden útil, pero artificial, en el caos. Un defensor de este tipo de idea fue Leopold Kronecker, profesor de matemáticas del siglo XIX en Alemania. Su credo se resume en la famosa declaración: "Dios creó los números naturales, todo lo demás es obra del hombre".
Otros argumentaron que aunque los números pueden o no existir físicamente, los enunciados matemáticos definitivamente no. Sus valores de verdad se basan en las reglas que los humanos crearon. Desde esta perspectiva, las matemáticas son, pues, un ejercicio de lógica inventado que no existe fuera del pensamiento consciente humano. Así, la matemática sería un lenguaje de relaciones abstractas basado en patrones discernidos por cerebros, construido para usar esos patrones e inventar un orden útil, pero artificial, en el caos. Un defensor de este tipo de idea fue Leopold Kronecker, profesor de matemáticas del siglo XIX en Alemania. Su credo se resume en la famosa declaración: "Dios creó los números naturales, todo lo demás es obra del hombre".
Durante la vida del matemático David Hilbert, hubo un impulso para establecer las matemáticas como una construcción lógica. Hilbert intentó axiomatizar toda la matemática como Euclides lo había hecho con la geometría. Él y otros que lo intentaron vieron las matemáticas como un juego profundamente filosófico, pero un juego al fin.
Henri Poincaré, uno de los padres de la geometría no euclidiana, comenzó a tratar con las superficies no planas de curvaturas hiperbólicas y elípticas demostrando que la geometría euclidiana (la de las superficies planas) no era una verdad universal, sino el resultado de la utilización de un grupo particular de reglas de juego.
En 1960, Eugene Wigner, premio Nobel de Física, acuñó la frase, "la irrazonable efectividad de las matemáticas" impulsando fuertemente la idea de que las matemáticas tienen su propia entidad y que fueron descubiertas por las personas. Wigner señaló que muchas teorías puramente matemáticas desarrolladas sin perspectiva de describir un fenómeno físico, han demostrado décadas o incluso siglos más tarde que son el marco necesario para explicar cómo el universo ha estado funcionando todo el tiempo.
La teoría de los números del matemático británico Godfrey Hardy, quien creyó que ninguno de sus trabajos sería útil en la descripción de los fenómenos del mundo real, ayudaron a fundar la criptografía. Otra pieza de su trabajo puramente teórico conocida como la ley de Hardy-Weinberg en la genética, ganó un premio Nobel.
Por su parte, el matemático italiano Fibonacci tropezó con la famosa sucesión que lleva su nombre mientras observaba el crecimiento de una población de conejos idealizada. La humanidad más tarde encontró esta sucesión de Fibonacci en diversas manifestaciones de la naturaleza, desde el patrón de crecimiento de un helecho hasta el trino de las aves, la disposición de los pétalos en las flores, la estructura del caparazón de ciertos moluscos y la espiral de una galaxia en el universo, por nombrar solo algunos entre cientos de ejemplos. La sucesión de Fibonacci es una de las formas matemáticas para encontrar el denominador común entre los patrones y los diseños de la naturaleza.
Henri Poincaré, uno de los padres de la geometría no euclidiana, comenzó a tratar con las superficies no planas de curvaturas hiperbólicas y elípticas demostrando que la geometría euclidiana (la de las superficies planas) no era una verdad universal, sino el resultado de la utilización de un grupo particular de reglas de juego.
En 1960, Eugene Wigner, premio Nobel de Física, acuñó la frase, "la irrazonable efectividad de las matemáticas" impulsando fuertemente la idea de que las matemáticas tienen su propia entidad y que fueron descubiertas por las personas. Wigner señaló que muchas teorías puramente matemáticas desarrolladas sin perspectiva de describir un fenómeno físico, han demostrado décadas o incluso siglos más tarde que son el marco necesario para explicar cómo el universo ha estado funcionando todo el tiempo.
La teoría de los números del matemático británico Godfrey Hardy, quien creyó que ninguno de sus trabajos sería útil en la descripción de los fenómenos del mundo real, ayudaron a fundar la criptografía. Otra pieza de su trabajo puramente teórico conocida como la ley de Hardy-Weinberg en la genética, ganó un premio Nobel.
Por su parte, el matemático italiano Fibonacci tropezó con la famosa sucesión que lleva su nombre mientras observaba el crecimiento de una población de conejos idealizada. La humanidad más tarde encontró esta sucesión de Fibonacci en diversas manifestaciones de la naturaleza, desde el patrón de crecimiento de un helecho hasta el trino de las aves, la disposición de los pétalos en las flores, la estructura del caparazón de ciertos moluscos y la espiral de una galaxia en el universo, por nombrar solo algunos entre cientos de ejemplos. La sucesión de Fibonacci es una de las formas matemáticas para encontrar el denominador común entre los patrones y los diseños de la naturaleza.
La teoría de nudos matemáticos -desarrollada alrededor del 1770 para describir la geometría de posición- fue utilizada en el siglo XX para explicar cómo el ADN contenido dentro del núcleo de las células se despliega a sí mismo durante el proceso de replicación.
También hay que considerar el trabajo no euclidiano de Bernhard Riemann en la década de 1850, que Einstein utilizó en el modelo de la relatividad general de un siglo más tarde.
Algunos de los matemáticos y científicos más influyentes de toda la historia estudiaron el tema que siempre inquietó a la humanidad.
¿Es la matemática una invención o un descubrimiento? ¿Es un constructo artificial o una verdad universal? Son preguntas tan profundas en el debate que a menudo toman un carácter espiritual. Si hay un número de árboles en un bosque, pero no hay nadie para contarlos, ¿existe ese número?
También hay que considerar el trabajo no euclidiano de Bernhard Riemann en la década de 1850, que Einstein utilizó en el modelo de la relatividad general de un siglo más tarde.
Algunos de los matemáticos y científicos más influyentes de toda la historia estudiaron el tema que siempre inquietó a la humanidad.
¿Es la matemática una invención o un descubrimiento? ¿Es un constructo artificial o una verdad universal? Son preguntas tan profundas en el debate que a menudo toman un carácter espiritual. Si hay un número de árboles en un bosque, pero no hay nadie para contarlos, ¿existe ese número?
Ver el siguiente video: https://youtu.be/X_xR5Kes4Rs
Así como el video te sugiere dos preguntas, que se hizo la humanidad respecto a la matemática, que otras preguntas te surgen a tí? Escríbelas.






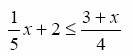 b)
b)